

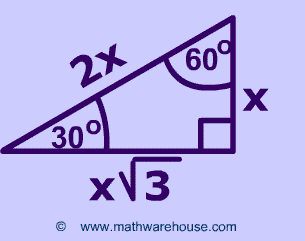
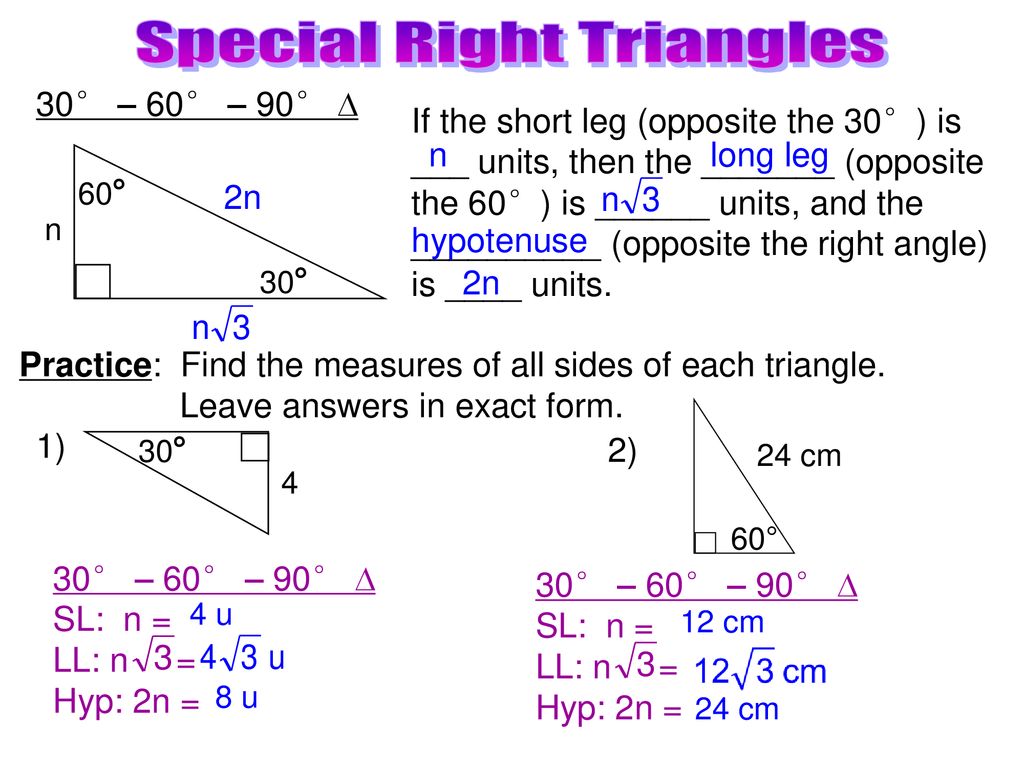
The ancient Greek mathematician and philosopher Pythagoras (500 B.C.) solved plenty of geometric conundrums including the theorem that now bears his name, which states that the hypotenuse (the diagonal line) of a right triangle is a square root which is equal to the squares of the other two sides.įor triangle (a,b,c) where the corner of (a|b) is 90 degrees, the measurements will satisfy the formula a2 + b2 = c2. Nature is Made of Triangles The humble triangle is the geometric shape without which most of our engineering would not be possible. It comes up surprisingly often in various contexts, from engineering to wave functions. The 30-60-90 triangle is the special case of a triangle with its ratios all in perfect proportion to each other. It is also possible to use trigonometric functions to find the rest of the triangle using any metric, given its rigid angle construction. And then you must know that the area of an equilateral triangle is equal to the area of a rectangle measuring X*Y. You might note that the 30-60-90 triangle is exactly one half of an equilateral triangle - a triangle with equal sides and 60 degree angles, where one side is X2, being the shortest side of our 30-60-90 triangle. The formulas for finding the rest of the triangle from just X are the following, where Y = the long side, Z = the hypotenuse, A = area, and P = perimeter: The Formulas of the 30-60-90: Given that X is the shortest side measure, we know we can measure out at the baseline for length X, turn an angle of 60 degrees, and have a new line that eventually intersects the line from the larger side at exactly 30 degrees. The 30-60-90 triangle is also a right triangle. Since our angles are rigorous, there is exactly one type of triangle we could give for any of these starting values. It works with a measure of any one side, or by inputting the area or perimeter. In our special right triangles calculator, we implemented five chosen triangles: two angle-based and three side-based.This calculator exists to compute the area of a triangle, where the three angles of the triangle measure 30, 60, and 90 degrees respectively, and only one other measurement is known.
There are many different rules and choices by which we can choose the triangle and call it special. Their areas are in geometric progression, according to the golden ratio. Right triangle, the sides of which are in a geometric progression (Kepler triangle).
#Special right triangles calculator 30 60 90 plus
Of course, the most important special right triangle rule is that they need to have one right angle plus that extra feature. Special right triangles are the triangles that have some specific features which make the calculations easier.


 0 kommentar(er)
0 kommentar(er)
